数据可视化：对数刻度

给定美国各个县 1980-2014 的酒精滥用致死率，请问如何对比出这两个年份的变化？

Don’t compare percentage change on a linear scale; use a log scale instead. -50% (0.5×) is as big a change as +100% (2×). 比较比例变化，不要在线性尺度上，而要在对数尺度上。因为减少了 50% 与增加了 100% 是一样大的变动。

上面的引文，是 5 月初 Mike Bostock 的一条推特，用的配图正对开头的问题。

当时我并没看明白他啥意思，留下了一个疑问。之后发现这条推引发了很多后续讨论，除了断断续续的松散对答，还有人专门花时间撰写了长文，比如 5 月 31 日至 6 月 14 日之间 Lisa Charlotte Rost 就在 Datawrapper Blog 上连作 3 篇关于「How to read a log scale」的文章来阐述自己的看法，分别是 Growth rate、The chart that can’t start at zero、What Mike Bostock means。对于这些讨论，Mike Bostock 在 6 月 16 日又写了一篇文章，亲自阐述那条推的含义，名为：Methods of Comparison, Compared。

这些文章提及了很多字面类似的概念，比如 Log Scale，Linear Scale，Percentage Change，Rate Change，Growth Rate 等等，大大小小还不少，那么，他们到底在谈些什么呢？我感觉上面的 Lisa 和 Mike 两人讲的测中稍有不同，归结起来大致是两项（还是有点绕）：

如何对比新旧数据之间比例的变化
如何展示对比结论

Lisa 行文更偏重于解释「何为 Log 刻度」以及「为什么、何时使用它」。第一篇引用了新西兰游客人数逐年变化的例子，很直观讲了对数刻度是什么以及使用它有什么好处；第二篇则引用了摩尔定律涉及的晶体管数量变化，讲了使用对数刻度的场合和需要注意的情况，比如坐标不可能从零开始等；第三篇则猜测了 Mike 原推的意思，为什么「-50%(0.5x) 也是 +100% 」以及她对百分之变化用线性还是对数坐标刻度的建议。

Mike 则综合强调了「对比和展示」。比如他以「全美滥用酒精致死情况」这一例子，2014 vs. 1980，他用了 4 种对比方式来展现经过 30 多年以后，每 10 万人中酒精滥用致死人数的变化：

并排做两幅图，让读者对着看
同一幅图展示两者差值 b − a
同一幅图展示两者相对变化 (a - b) / a
同一幅图展示两者比例变化 a / b，并取对数

哪一个最好呢？none of them，他说。因为方法并无绝对高下之分，按需选择最合适的。比如上面的例子，重点若是为了直接表现个体死亡的可能性（因为源数据统计的就是每年每 10 万人中的死亡个数），他认为第 2 种 b - a 取数值差异的方式就很不错；但如果目的是为了展示增长的比例，第 4 种方案应该会更好一些。

动手玩

Mike Bostock 是 D3 的作者，他演示用的代码都是 D3，操作平台也是自己的新项目 Observable。我还没有玩过 D3，以下内容如有涉及绘图，采用的将会是最近在玩的 Altair（其实底层也还是 vega-lite 和 D3），跑在本地 Jupyter Notebook，或是 nteract 或是 Google Colab 上都行，没什么区别。点击 ▶︎ 展开代码。

1. 新西兰的游客


import numpy as np
import pandas as pd
import altair as alt

nzt = pd.read_csv('data-OHT21.csv')

#
# linear scale
#
alt.Chart(nzt).mark_line().encode(
  x=alt.X('yearmonth(Date):T', axis=alt.Axis(format='%Y', title=None)),
  y=alt.Y('Close', title=None)
).properties(
  width=920
)

#
# log scale
#
alt.Chart(nzt).mark_line().encode(
  x=alt.X('yearmonth(Date):T', axis=alt.Axis(format='%Y', title=None)),
  y=alt.Y('Close', title=None)
).properties(
  width=920
)

linear scale

log scale

上面两幅图背后的数据是一模一样的，注意 Y 轴，第一幅是比较常见的线性坐标刻度，第二幅则是以 10 为底的对数刻度。在上面这个例子中，其显而易见的一个好处就是：它「看到」了一个普通线性刻度看不到情况——二战期间的游客大幅减少了。

所以，其实这里用到了对数的第一个特性：在数据呈指数增长的情况下，在坐标系中使用作为指数的逆函数的对数刻度，使陡峭的曲线变得平缓。比如同样限宽 100 的两把尺子，一条为常见的线性刻度，一条为以 10 为底的对数刻度，如果画出来，则如下图，0-10，10-20，20-30 占的距离一样，这是线性的；原点（不能为 0）到 1，1 到 10，10 到 100 距离是一样的，这是对数的。

linear

这也是 Mike 说的「-50%(0.5x) 即 +100% 」的含义所在，假如 A 地死亡人数由 4 个上升到了 8 个，B 地则由 8 个减少到了 4 个，如果计算百分比变化，A 地是上升了 100%，B 地是减少了 50%，可视化出来，画到坐标轴上，占地距离差异很大，然而实际上却只是两个数调了个位，4-8，8-4 怎么就不一样了呢，正是为了这个问题，Mike 才发的开头的推。他的建议是，取比例变化的对数，即 log(a/b)，因为无论底数如何，log(4/8) 和 log(8/4) 的绝对值都是一样的，一正一负正好对称。

In [1]: import math

In [2]: math.log(8/4, math.e)
Out[2]: 0.6931471805599453

In [3]: math.log(4/8, math.e)
Out[3]: -0.6931471805599453

这一对值，体现到坐标距离或是地图颜色上，就合理了。制作直角坐标系图表的工具里，像 Excel、iWorks Numbers、Google/Yahoo 的一些在线工具，基本都提供了对数刻度这一选项。

如何对比搞清楚了，怎么展示呢？这也是这个例子特殊的地方，它是个 choropleth 地图，不是柱状图、折线图等直角坐标系，其实也差不多，同样考虑两个东西：

一个是图例 Legend，本例需要颜色对称，冷色表降，暖色表升，范围取 [1/max(a/b), 1, max(a/b)]。

颜色图例


alt.Chart(deaths).mark_tick().encode(
    color=alt.Color('ratio_change:Q', scale=alt.Scale(type='log', domain=domain, range=['steelblue', 'white', 'red']), legend=alt.Legend(orient='bottom-left', format='.2r', offset=0, title=None))
).configure_view(strokeWidth=0).configure_legend(gradientWidth=720)

linear

另一个是坐标填充，本例坐标是 geoshape，略微复杂，下回专门写，先用下图做个示意，就是一个对应关系。

填充示意


deaths2 = deaths[deaths['location_name'].str.contains('County')].sample(n=30)

alt.Chart(deaths2).mark_square(size=400).encode(
    x=alt.X('location_name:O', title=None),
    color=alt.Color('ratio_change:Q', scale=alt.Scale(type='log', domain=domain, range=['steelblue', 'white', 'red'], nice=True), legend=None)
).properties(
    width=720
).configure_view(strokeWidth=0)

linear

合起来，就是 Mike 的结果。

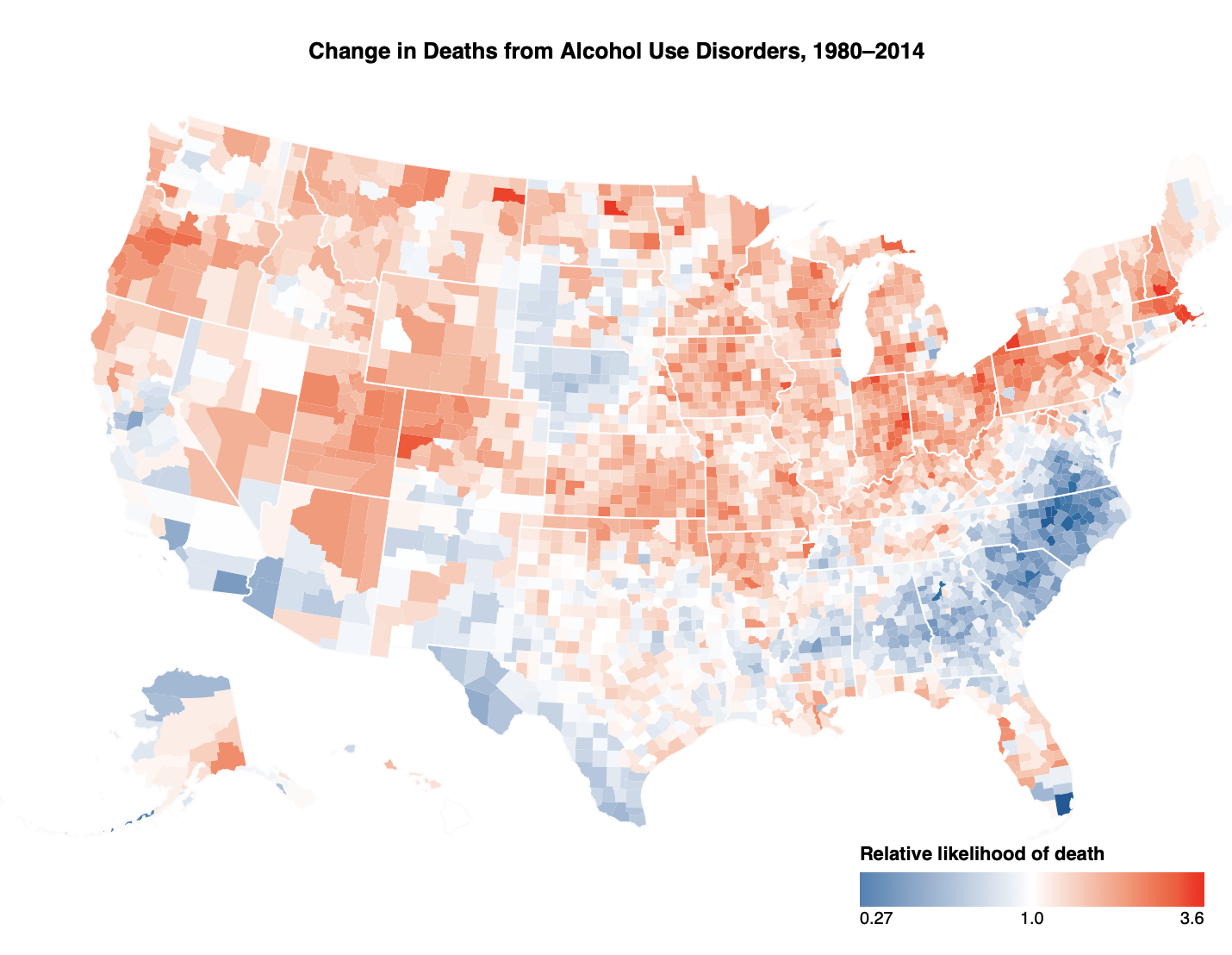
death map

美国各显酒精滥用致死率变化，1980-2014


import math
import numpy as np
import pandas as pd
import altair as alt
from vega_datasets import data

counties = alt.topo_feature('./data/cb_2017_us.json', 'counties')
states = alt.topo_feature('./data/cb_2017_us.json', 'states')
temp = pd.read_csv('./data/deaths.csv')
deaths = pd.read_csv('./data/data-OXy0O.csv', skiprows=1, names=['fips_code', 'percent_change', 'location_name'], dtype={'fips_code': 'str', 'percent_change': np.float64, 'location_name': 'str'})

deaths['ratio_change'] = deaths['percent_change'].apply(lambda x: (x + 100) / 100)

max_ratio = min(max(temp['2014'] / temp['1980']), max(temp['1980'] / temp['2014']))
domain = [(1 / max_ratio), 1, max_ratio]
title = 'Change in Deaths from Alcohol Use Disorders, 1980–2014'

counties_choropleth = alt.Chart(counties).mark_geoshape().encode(
    color=alt.Color(
        'ratio_change:Q',
        scale=alt.Scale(type='log', domain=domain, range=['steelblue', 'white', 'red'], interpolate='lab', zero=False),
        legend=alt.Legend(orient='bottom-right', title='Relative likelihood of death', format='.2r')
    ),
    tooltip=alt.Tooltip('location_name:O')
).transform_lookup(
    lookup='properties.GEOID',
    from_=alt.LookupData(deaths, 'fips_code', ['ratio_change', 'location_name'])
).project(
    type='albersUsa'
).properties(
    width=720,
    height=560,
    title=alt.TitleParams(title, orient='top', offset=-40)
)

states_choropleth = alt.Chart(states).mark_geoshape(filled=False, stroke='#fafafa', strokeWidth=1).encode()
death_map = counties_choropleth + states_choropleth
death_map.configure_legend(gradientWidth=200)